In matematica, la serie armonica è la sommatoria infinita delle frazioni unitarie o, equivalentemente, dei reciproci dei numeri naturali:
- ∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + … {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\dots }
Deve il suo nome al fatto che gli armonici prodotti da un corpo vibrante hanno rapporti di lunghezza d’onda con il suono fondamentale che si possono esprimere con gli addendi della serie.
La successione delle sue somme parziali è monotona e strettamente crescente rispetto alla variabile rappresentata dal numero di addendi, e il suo carattere è divergente: per un m {\displaystyle m} 


Il fatto che la serie diverga può non essere evidente a prima vista, poiché l’ultimo termine delle somme parziali tende a zero al crescere del numero di addendi. Esistono tuttavia molte semplici dimostrazioni della divergenza della serie.
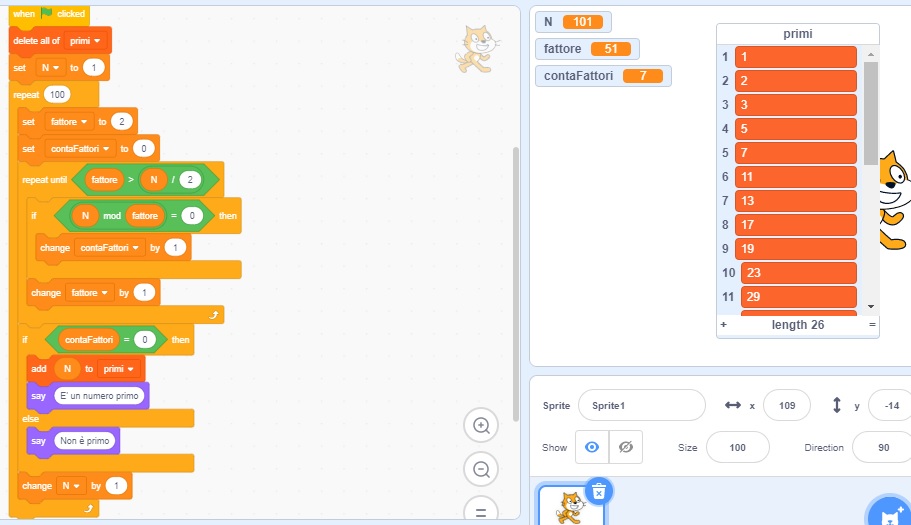
Ecco il programmino che puoi modificare per sperimentare la sua divergenza.
include the below at bottom of the Blog Post or Website